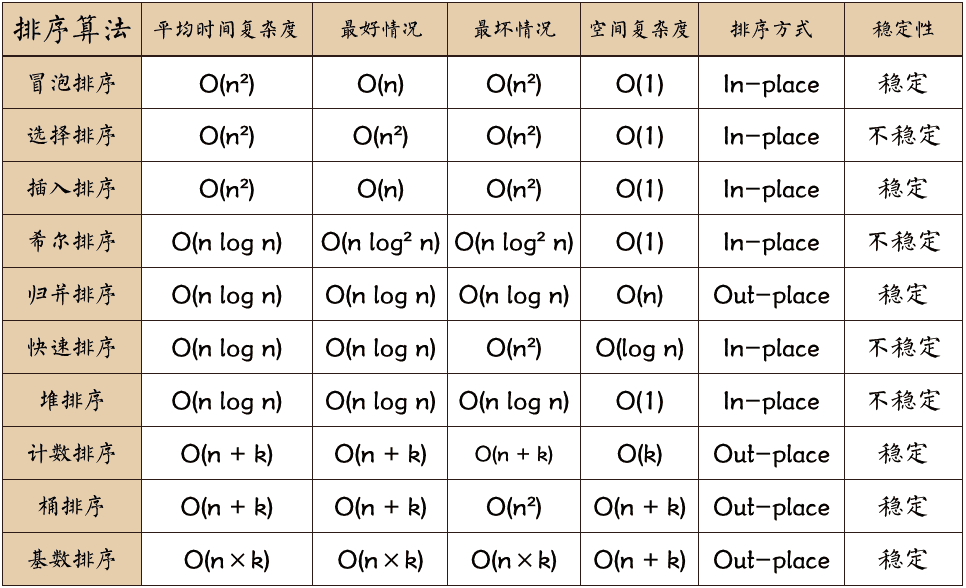
本文介绍排序算法,常见的排序算法主要有冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、堆排序和基数排序。
1. 冒泡排序
冒泡排序,就是相邻元素比较,【根据升序还是降序】如果不满足顺序要求,则交换。一次遍历就会找到一个最大值/最小值。遍历的过程中就相当于冒泡。有n个元素,就需要找n-1次最大值/最小值。最终就会达到总体排序。代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
public void bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
for (int j = 1; j < array.length - i; j++) {
if(array[j] < array[j-1]) {
array[j] = array[j] + array[j-1];
array[j-1] = array[j] - array[j-1];
array[j] = array[j] - array[j-1];
}
}
}
}
|
2. 选择排序
选择排序,其实就是在冒泡的基础上,无需每次都交换,只需要维持一个变量,使得其是最大值/最小值即可,最终遍历到最后一个位置【当前遍历的序列】,将最小值/最大值放入该位置即可。代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
public void selectSort(int[] array) {
int max = 0;
for (int i = 0; i < array.length - 1; i++) {
max = 0;
for (int j = 1; j < array.length - i; j++) {
if(array[j] > array[max]) max = j;
}
if(max != array.length - 1 - i) {
array[array.length - 1 - i] += array[max];
array[max] = array[array.length - 1 - i] - array[max];
array[array.length - 1 - i] -= array[max];
}
}
}
|
3. 插入排序
插入排序,就是将已有的序列是排好序的,那么后续再插入元素的时候,可直接比较交换位置即可。换句话说,就是将元素从前到后形成的子数组,逐个排序。有点像动态规划。代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
for (int j = i; j > 0; j--) {
if(array[j] < array[j-1]) {
array[j] += array[j-1];
array[j-1] = array[j] - array[j-1];
array[j] = array[j] - array[j-1];
}
}
}
}
|
4. 希尔排序
仔细观察插入排序,如果插入的值是最小值,显然会进行很多次移动。可以将数组分成若干个序列,这样对每个序列进行插入排序,这样,一个元素,相对于整个数组来说,直接一步移动到较远的位置,减少移动次数。之后序列数再减半,直到为1为止。
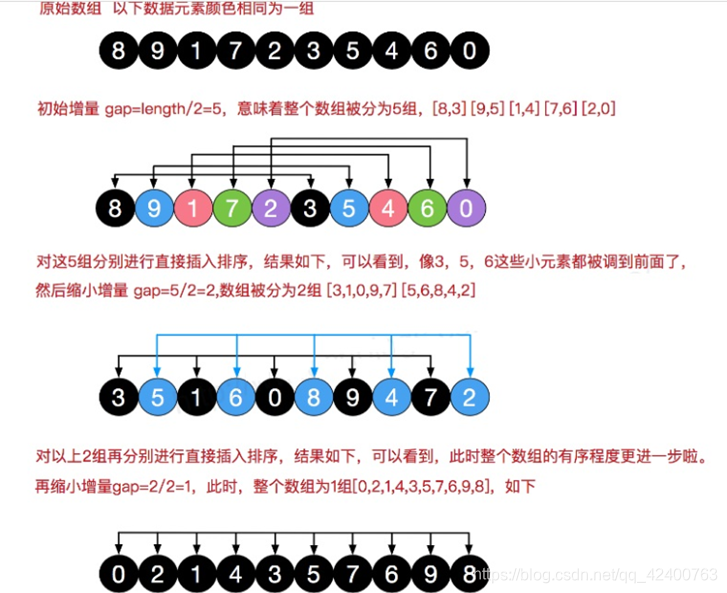
代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public void shellSort(int[] array) {
int temp = 0;
int incre = array.length;
while(true){
incre = incre / 2;
for(int k = 0; k < incre; k++){
for(int i = k + incre; i < array.length; i += incre){
for(int j = i; j > k; j -= incre){
if(array[j] < array[j-incre]){
temp = array[j-incre];
array[j-incre] = array[j];
array[j] = temp;
}else{
break;
}
}
}
}
if(incre == 1){
break;
}
}
}
|
5. 快速排序
快速排序采用的是分治的思想。选定一个数,对数组进行排序,小于它的放在左边,大于它的放在右边。之后分别在左右两边继续按照此方法做。代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
public void quickSort(int[] array, int start, int end) {
if(start >= end) return;
int head = start + 1;
int tail = end;
while(head < tail) {
while(head < tail && array[head] <= array[start]) head++;
while(tail > head && array[tail] > array[start]) tail--;
if(head < tail) {
array[head] += array[tail];
array[tail] = array[head] - array[tail];
array[head] -= array[tail];
}
}
if( head - 1 > start) {
array[start] += array[head-1];
array[head-1] = array[start] - array[head-1];
array[start] -= array[head-1];
quickSort(array, start, head - 2);
quickSort(array, head, end);
}
}
|
6. 归并排序
归并排序就是将两个有序数组合并。从而使得整合数组有序。感觉和希尔排序类似。只不过归并排序以分治法的角度划分数组,而不是从逻辑上划分等差的子序列。代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
public void mergeSort(int[] array, int start, int end) {
if(start >= end) return;
if(end - start == 1) {
if(array[end] < array[start]) {
array[end] += array[start];
array[start] = array[end] - array[start];
array[end] -= array[start];
}
return;
}
int mid = (start + end) / 2;
mergeSort(array, start, mid);
mergeSort(array, mid+1, end);
int firstStart = start;
int nextStart = mid + 1;
int[] temp = new int[array.length];
int index = firstStart;
while(firstStart <= mid && nextStart <= end) {
if(array[firstStart] <= array[nextStart]) {
temp[index] = array[firstStart];
firstStart++;
} else {
temp[index] = array[nextStart];
nextStart++;
}
index++;
}
while(firstStart <= mid) {
temp[index++] = array[firstStart++];
}
while(nextStart <= mid) {
temp[index++] = array[nextStart++];
}
for (int i = start; i <= end; i++) {
array[i] = temp[i];
}
}
|
7. 计数排序
这种排序算法利用空间来换时间。定义数组,数组大小为给定的数组的最大值和最小值的差值。这样在遍历数组的时候,可根据元素值来给新数组对应下标元素赋值,表示该元素的个数。最终遍历新数组,只要不是0,就说明有元素,值就是最小值+下标。代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
public void countSort(int[] array) {
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int i = 0; i < array.length; i++) {
if(array[i] < min) min = array[i];
if(array[i] > max) max = array[i];
}
int[] result = new int[max - min + 1];
Arrays.fill(result, 0);
for (int i = 0; i < array.length; i++) {
result[array[i] - min] += 1;
}
int index = 0;
for (int i = 0; i < result.length; i++) {
while(result[i] != 0) {
array[index] = min + i;
result[i] -= 1;
index++;
}
}
}
|
8. 堆排序
堆排序指的是利用堆数据结构,堆数据结构可看成是完全二叉树,且满足根节点大于左右子节点(大顶堆),或者根节点小于左右子节点(小顶堆)。
将数组构建成一个大顶堆之后,根节点就是最大值。然后将剩余元素继续构建大顶堆,此时根节点就是次大值。继续下去,可得到所有的最大值,即有序。
那么怎么将数组看成堆呢?其实可将数组看成是完成二叉树的层序遍历。这样就是一个堆了。之后,找到最大值,都将其放到当前序列的最后一个位置。继续将剩余位置的元素构建大顶堆。
注意,构建大顶堆,需要自底向上。代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public void heapSort(int[] array) {
for (int i = array.length - 1; i > 0; i--) {
maxHeapFix(array, 0, i);
array[i] += array[0];
array[0] = array[i] - array[0];
array[i] -= array[0];
}
}
public void maxHeapFix(int[] array, int start, int end) {
for (int i = end; i >= start; i--) {
if(2 * i + 1 <= end && array[i] < array[2 * i + 1]) {
array[i] += array[2 * i + 1];
array[2 * i + 1] = array[i] - array[2 * i + 1];
array[i] -= array[2 * i + 1];
}
if(2 * i + 2 <= end && array[i] < array[2 * i + 2]) {
array[i] += array[2 * i + 2];
array[2 * i + 2] = array[i] - array[2 * i + 2];
array[i] -= array[2 * i + 2];
}
}
}
|
9. 桶排序
前面的计数排序是将相同的值放入到同一个桶中,这样的话,空间开销较大。其实可设计一个映射函数,利用某种规则,将若干个数放到同一个桶中。使得总体有序,然后再将桶内元素进行排序,使得局部有序,最终总体有序。和分治法类似。
但是桶排序在划分桶的时候,并不是用的比较法,而是采用其他的规则,比如哈希函数等等。
10. 基数排序
基础排序可以看成是多次计数排序。将元素,分别按照个位、十位、百位等依次采用计数排序。



