1. question: 删除二叉搜索树中的节点(中等)
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/delete-node-in-a-bst
示例 1:

1
2
3
4
5
| 输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
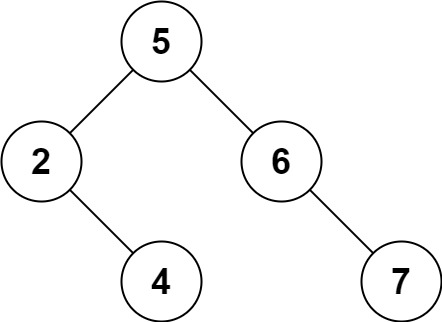
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
|
示例 2:
1
2
3
| 输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
|
示例 3:
1
2
| 输入: root = [], key = 0
输出: []
|
提示:
1
2
3
4
5
| 节点数的范围 [0, 104].
-105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
-105 <= key <= 105
|
2. answers
这道题,重点似乎是:删除二叉搜索树的根节点,并重构它。总体思路是:
- 找到要删除的节点
- 该节点及其子节点就是一棵二叉搜索树,然后将其重构。
- 将重构后的二叉搜索树插入到原来的位置上,因此在找节点的时候,要保留其父节点。
其实重点是如何重构一棵二叉搜索树。这棵二叉搜索树有多种情况:
只有根节点
删除该节点,返回空即可
只有左子树
返回其左子树即可。
只有右子树
返回其右子树即可
普通二叉搜索树
这里的重构二叉搜索树,其实指的就是找到一个根节点。而我们知道,二叉搜索树是中序递增的,因此,只需要找到左子树的最大值,或者右子树的最小值即可。将两个任意一个作为根节点就行。
以找右子树的最小值为例。最小值一定是左节点。只需要遍历即可。在遍历的时候,一定要保留其父节点,因为最小值是作为最终的根节点,那么该父节点的左节点(也就是最小值)就要设为null。
下面就是如何将最小值作为根节点。
- 最小值的左节点一定是空,因为如果不是空,那么它就不是最小值。所以作为最终的根节点,新的左子树就是原来的左子树;
- 那么新的右子树怎么确定呢?因为最小值可能存在右节点,也可能不存在右节点。其实最小值的右节点一定是小于原来右子树的根节点的。只需要遍历右节点,将原来右子树作为右节点的右子树即可。
代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
|
public class Solution_0074 {
public int tag;
public TreeNode constructTree(TreeNode tn) {
if(tn.left == null && tn.right == null) return null;
if(tn.left == null && tn.right != null) return tn.right;
if(tn.left != null && tn.right == null) return tn.left;
TreeNode left = tn.left;
TreeNode right = tn.right;
if(right.left == null) {
right.left = left;
return right;
}
TreeNode temp = right;
TreeNode tempPar = right;
while(temp.left != null) {
tempPar = temp;
temp = temp.left;
}
tempPar.left = null;
temp.left = left;
TreeNode tempRight = temp;
while(tempRight.right != null)
tempRight = tempRight.right;
tempRight.right = right;
return temp;
}
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null) return null;
TreeNode result = root;
TreeNode pre = root;
while(root != null) {
if(root.val > key) {
pre = root;
root = root.left;
}
else if(root.val < key) {
pre = root;
root = root.right;
}
else {
if(pre.left == root) tag = -1;
if(pre.right == root) tag = 1;
break;
}
}
if(root == null) return result;
TreeNode sub = constructTree(root);
if(pre == root) return sub;
if(tag == -1) pre.left = sub;
if(tag == 1) pre.right = sub;
return result;
}
public static void main(String[] args) {
System.out.println();
TreeNode tn1 = new TreeNode(0);
Solution_0074 s = new Solution_0074();
TreeNode result = s.deleteNode(tn1, 0);
Queue<TreeNode> queue = new LinkedList<>();
if(result == null) return;
queue.offer(result);
while(queue.size() > 0 ) {
int length = queue.size();
while(length-- > 0) {
result = queue.poll();
System.out.print(result.val + "\t");
if(result.left != null) queue.offer(result.left);
if(result.right != null) queue.offer(result.right);
}
System.out.println();
}
}
}
|
改进一下思路:其实在找新的根节点的时候,没必要是左子树的最大值或者右子树的最小值。只需要将原始左子树作为原始右子树最小值的左节点即可,原始右子树的根节点为新的根节点。或者原始右子树组委原始左子树最大值的右节点。
因为要删除的根节点,其左右子树都是二叉搜索树,只需要以最简单的形式将二者融合即可。右子树一定是大于根节点的,而根节点一定是大于左子树的最大值节点的。所以只需要找到左子树的最大值节点,将右子树拼接为最大值节点的右节点即可(相当于插入操作)。
代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
public TreeNode constructTree(TreeNode tn) {
if(tn.left == null && tn.right == null) return null;
if(tn.left == null && tn.right != null) return tn.right;
if(tn.left != null && tn.right == null) return tn.left;
TreeNode left = tn.left;
TreeNode right = tn.right;
TreeNode temp = right;
while(temp.left != null) {
temp = temp.left;
}
temp.left = left;
return right;
}
|
3. 备注
参考力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 (leetcode-cn.com),代码随想录 (programmercarl.com)。



